ACTIONS CONSEIL ECOLE-COLLEGE 2014-2015
|
Groupe de réflexion constitué de :
- MC Cottard, Principale du Collège Le Petit Prétan
- Cécile Bourgeois, professeure de mathématiques
- Christine Favier, Conseillère Pédagogique Circonscription de Tournus
- Pierre Gangloff, professeur des écoles à Jambles ( 12 cycle 3)
- Floranne Lucas, professeure des écoles à Givry (26 CM2)
Manuels scolaires utilisés en primaire : Outils pour les Maths (Ed. Magnard) et Math Elem (Ed. Belin)
Comment se déroule une heure de cours au collège ?
Sur une heure de cours, les exercices à faire à la maison sont corrigés, la leçon est abordée, et il reste environ ¼ d’heure d’autonomie sur de nouveaux exercices. Certains exercices sont obligatoires et d’autres accessibles aux élèves les plus rapides (gestion de l’hétérogénéité).
Les évaluations sont prévues pour durer environ 30 min. mais certains élèves ont besoin de l’heure complète, ce qui leur est accordé. Les évaluations se déroulent dans le plus grand silence, et sans échange de matériel.
Les élèves dyslexiques choisissent leurs exercices. Leur note est proportionnellement recalculée sur 20, puisqu’ils ne peuvent pas être aidés par une reformulation orale (compétence à évaluer) ou un temps supplémentaire.
Pour information, les élèves reçoivent 1 heure hebdomadaire d’aide personnalisée (AP) en mathématiques, avec échange de service (deux professeurs de mathématiques). Travail sur le dessin du panda (figure géométrique) et sur les tableaux de commandes (calculer pour donner du sens).
Constats liés à l’aspect matériel et spatial
- A l’école, les traces écrites des élèves sont sur cahier, ou dans un classeur afin de
préparer au collège et d’alléger le cartable.
Au collège, les élèves travaillent sur des cahiers au format A4.
→ Apprendre à gérer un classeur (tri, rangement régulier) n’est donc pas une priorité
en CM2. - Outils de géométrie : les équerres triangulaires et graduées sont sources de fausses
représentations à l’école comme au collège, le compas est trop peu utilisé pour
reporter des longueurs à l’école, il faudrait aussi privilégier l’usage de la règle non
graduée (difficile à trouver dans le commerce). - La présentation des problèmes est semblable avec une colonne servant aux calculs.
Constats sur l’approche des nouveaux concepts
En primaire, les enseignants affirment que les élèves ont de plus en plus besoin de manipuler pour assimiler un concept. Au collège, la manipulation existe aussi quand la leçon s’y prête. (« manipulation » et/ou « visualisation », par exemple pour les horaires avec des horloges).
La place donnée à la manipulation reste cependant insuffisante car chronophage à court terme, mais il est constaté qu’une notion abordée par manipulation s’acquiert et se consolide plus vite et plus durablement.
Ce besoin de manipuler pourrait trouver son explication dans le fait que les élèves sont de plus en plus assistés, ou au contraire livrés à eux-mêmes très jeunes, et qu’ils partagent de moins en moins d’activités avec leurs parents. Il leur manque donc des référentiels liés à l’expérimentation et à la manipulation. (exemple de la recette au cycle 3 qui aborde aussi
bien les mélanges, la pesée et les conversions que la proportionnalité).
A Jambles, les élèves travaillent sur les stratégies de résolution : les élèves construisent un panel de stratégies et peuvent choisir la plus adaptée en fonction du contexte ou de l’élève.
A Givry, l’enseignante met l’accent sur la terminologie. Dans la résolution de problèmes, c’est très difficile. Le lecture de consignes est très importante.
Constats sur les points de résistance observés au collège
En numération :
– arrondir un nombre ;
– donner un encadrement au 10e ;
– donner un ordre de grandeur.
En géométrie (le programme est le même au cm2 et en 6e) :
– le point est l’intersection de deux droites, il se représente par une croix ;
– le cercle est l’ensemble des points à égal distance du centre ;
– au collège, la formule de la longueur est exprimée par « diamètre x π » ;
– le codage : (AB) pour droite, [AB] pour segment…
– la notion de plan.
Divergences de pratiques
– Le papier millimétré et la droite numérique sont très utilisés en primaire pour travailler sur les fractions et les nombres décimaux. Au collège, c’est un support rare.
– A l’école, un élève vérifie la nature d’une figure géométrique qui lui est soumise avec ses outils de géométrie et note ensuite le codage correspondant sur la figure. Au collège, si le codage n’est pas noté, cela signifie qu’il ne faut pas se servir de la propriété dans la démonstration attendue. Cela déconcerte les élèves.
– Opérations : les quatre opérations sont revues, sans s’appesantir sur les techniques (sauf besoins identifiés), mais en approfondissant le calcul avec décimaux. La place des retenues dans les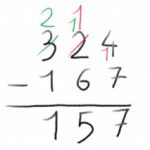 
soustractions et multiplications est très variable d’une classe à l’autre de CM2, et de l’école au collège. La technique opératoire de la soustraction développée au collège est celle illustrée ci-contre (pour faciliter la transition avec les calculs d’horaires). En sixième, l’élève revoit la division comme au CM2 et enchaîne avec l’étape du diviseur décimal.
Gestion des devoirs par les parents
La demande des enseignants est que les parents s’intéressent et échangent avec leur enfant sur ce qui a été fait à l’école et au collège. Ils ne demandent pas que les parents s’investissent davantage.
L’enfant sait ce qui est obligatoire ou non, c’est un « contrat » avec lui.